复兴高级中学2018-2019学年度第一学期高二期末考试数学试题
1、填空题
1.计算![]() _________.
_________.
2.直线![]() 与直线
与直线![]() 的夹角大小为________.
的夹角大小为________.
3.在复平面,复数![]() 对应的点坐落于第_______象限.
对应的点坐落于第_______象限.
4.直线![]() 被圆
被圆![]() 截得的弦长为_______.
截得的弦长为_______.
5.![]() 为椭圆C:
为椭圆C:![]() 的焦点,点P为椭圆C上一点,则
的焦点,点P为椭圆C上一点,则![]() 的周长为________.
的周长为________.
6.计算: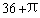 ______.
______.
7.若![]() 满足约束条件
满足约束条件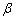 则
则![]() 的最大值为_______.
的最大值为_______.
8.“![]() ”是“关于
”是“关于![]() 的实系数方程
的实系数方程![]() 有虚根”的_________条件.
有虚根”的_________条件.
9.已知双曲线C:![]() 的右顶点为A,以A为圆心,
的右顶点为A,以A为圆心,![]() 为半径作圆与双曲线的一条渐近线交于M、N两点,若∠MAN=60°,则
为半径作圆与双曲线的一条渐近线交于M、N两点,若∠MAN=60°,则![]() _______.
_______.
10.设复数![]() 满足
满足![]() 则
则![]() _______.
_______.
11.已知曲线C:![]() 直线
直线![]() 若对于点A
若对于点A![]() 存在C上的点P和
存在C上的点P和![]() 上的点Q使得
上的点Q使得![]() 则实数
则实数![]() 取值范围为________.
取值范围为________.
12.已知点E是抛物线C:![]() 的对称轴与准线的交点,点F是抛物线的焦点,点P在抛物线上,在△EFP中,
的对称轴与准线的交点,点F是抛物线的焦点,点P在抛物线上,在△EFP中,![]() 的最大值为_________.
的最大值为_________.
2、选择题
13.下列关于双曲线C:![]() 的判断,正确的是
的判断,正确的是
A.渐近线方程为![]() B.焦点坐标为
B.焦点坐标为![]()
C.实轴长为12 D.顶点坐标为![]()
14.设有下面四个命题:
若复数![]() 满足
满足![]() 则
则![]()
若复数![]() 满足
满足![]() 则
则![]()
若复数![]() 满足
满足![]() 则
则![]()
若复数![]() 满足
满足![]() 则
则![]()
则正确命题的个数为
A.1 B.2 C.3 D.4
15.记椭圆![]() 围成的地区为
围成的地区为![]() 当点
当点![]() 分别在
分别在
![]() 上时,
上时,![]() 的最大值分别是
的最大值分别是![]() 则
则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
16.对于平面上点P和曲线C,任取C上一点Q,若线段PQ的长度存在最小值,则称该值为点P到曲线C的距离,记作![]() 若曲线C是边长为6的等边三角形,则点集
若曲线C是边长为6的等边三角形,则点集
![]() 所表示图形的面积为
所表示图形的面积为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3、解答卷
17.![]() 是关于
是关于![]() 的方程
的方程![]() 的一个根.
的一个根.
若![]() 且
且![]() 求实数
求实数![]() 的值;
的值;
若![]() 且
且![]() 为虚数,求实数
为虚数,求实数![]() 的值。
的值。
18.已知抛物线C的顶点在坐标原点,准线![]() 的方程为
的方程为![]() 点P在准线
点P在准线![]() 上,纵坐标为
上,纵坐标为
![]() 点Q在
点Q在![]() 轴上,纵坐标为
轴上,纵坐标为![]()
求抛物线C与直线PQ的方程;
求证:直线PQ恒与一个圆心在![]() 轴上的定圆M相切,并求出该圆M的方程。
轴上的定圆M相切,并求出该圆M的方程。
19.点P在![]() 轴上的投影为H,若A,B,且
轴上的投影为H,若A,B,且![]()
求P点的轨迹方程;
过B的直线在![]() 轴下方交P点轨迹于C、D两点,求CD中点与Q连成直线的斜率的取值范围。
轴下方交P点轨迹于C、D两点,求CD中点与Q连成直线的斜率的取值范围。
20.在直角坐标系![]() 中,曲线C的参数方程为
中,曲线C的参数方程为![]() 直线
直线![]() 的方程为
的方程为
![]()
若![]() 求曲线C与直线
求曲线C与直线![]() 的交点坐标;
的交点坐标;
若曲线C上的点到直线![]() 的距离最大值为
的距离最大值为![]() 求实数
求实数![]() 的值;
的值;
曲线C与![]() 轴的交点由上至下分别为
轴的交点由上至下分别为![]() P为曲线C上异于
P为曲线C上异于![]() 的一动点,若点Q满足:
的一动点,若点Q满足:![]() 判断
判断![]() 的与
的与![]() 面积之比是不是为定值,如果是,求出该定值;若不是,请说明理由。
面积之比是不是为定值,如果是,求出该定值;若不是,请说明理由。
21.已知二次曲线![]() 的方程为
的方程为![]()
分别求出方程表示椭圆和双曲线的条件;
若抛物线![]() 与
与![]() 共焦点,求抛物线L上的动点A到点
共焦点,求抛物线L上的动点A到点![]() 的最小值
的最小值![]()
![]() 为正常数,且
为正常数,且![]() 是不是存在两条曲线
是不是存在两条曲线![]() 其交点P与点
其交点P与点![]() 满足
满足![]() 若存在,求
若存在,求![]() 的值;若没有,请说明理由。
的值;若没有,请说明理由。







